0x00 前言#
起因是这样的,马上就要回所了,计算所的宿舍选择有三项,苏州街、青年公寓和科一招,其中科一招应该是较差的,苏州街住宿条件最好,但是 6 人间,并且通勤时间较长,青年公寓就显得比较 OK。
而青年公寓和苏州街的名额有限,往往通过抽签的方式,而最传统的抽签方式就是抢红包,笔者所在的实验室采取的策略是赢家通吃,也就是获得微信红包的 Top K 的获得更好的住宿。
0x01 分析#
毕导在 2020 年就做过了微信抢红包的分析 BV1z7411e7qB ,得到的结论是,所有人的期望都是相同的,但是越往后越容易抽到“大红包”,方差会变大。
由此也有了获得运气王的概率:
而在这个条件下,我们希望获得了可以不是运气王,Top K 就可以了,所以这算是毕导工作的一个 Incremental work。
0x02 模拟#
从毕导的视频中可以看到,微信红包的金额是[0.01, 剩余金额平均值的 2 倍],于是乎,笔者用 ChatGPT 写了个程序模拟,自己修改了一下 BUG,这里我们只计算至多 20 个人的至多 Top10,模拟了 100000 次。
但是有一些坑需要注意,首先,抢到的金额应当是保留两位小数的,同时,如果是最后一个人,那么他抢到的金额应当是剩余的金额。
代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
import random
import matplotlib.pyplot as plt
# 模拟参数
num_trials = 100000
def simulate_red_envelope (num_users):
total_amount = 100.0
red_envelope = [0.0 ] * num_users
for i in range (num_users):
remaining_envelope = num_users - i
remaining_amount = total_amount - sum (red_envelope)
avg_amount = remaining_amount / remaining_envelope
max_amount = min (avg_amount * 2 , remaining_amount)
amount = (
random.uniform(0.01 , max_amount)
if remaining_envelope > 1
else remaining_amount
)
amount = round (amount * 100 ) / 100.0
red_envelope[i] = amount
return red_envelope
def calculate_topk_probability (num_users, num_trials):
probabilities = []
for k in range (1 , min (num_users, 10 )):
results = [0 ] * num_users
for _ in range (num_trials):
red_envelope = simulate_red_envelope(num_users)
sorted_envelope = sorted (
range (num_users), key=lambda x: red_envelope[x], reverse=True
)
topk = sorted_envelope[:k]
# 统计获得 topk 的概率
for i in range (k):
results[topk[i]] += 1
probabilities.append([result / num_trials for result in results])
return probabilities
def plot_probability (probabilities):
num_users = len (probabilities[0 ]) if len (probabilities) > 0 else 0
k_values = list (range (1 , min (num_users, 10 )))
# 绘制 k 个子图
plt.figure(figsize=(4 * len (k_values) + 4 , 4 ))
for i, k in enumerate (k_values):
ax = plt.subplot(1 , len (k_values), i + 1 )
ax.plot(range (1 , num_users + 1 ), probabilities[i], label="Probability" )
print (probabilities[i], k)
ax.set_xlabel("Rank" )
ax.set_xlim(1 , num_users)
# 只显示整数坐标
ax.set_xticks(range (1 , num_users + 1 ))
ax.set_ylabel("Probability" )
ax.set_ylim(0 , 1 )
# Title
ax.set_title("Probability of Top {} Amounts" .format(k))
# plt.xlabel("Rank")
# plt.xlim(1, num_users)
# # 只显示整数坐标
# plt.xticks(range(1, num_users + 1))
# plt.ylabel("Probability")
# plt.ylim(0, 1)
# plt.title("Probability of Top K Amounts")
# plt.legend()
plt.savefig("red_envelope_probability_N {} _K {} .png" .format(num_users, k))
for N in range (2 , 21 ):
# 模拟抢红包并计算概率
probabilities = calculate_topk_probability(num_users=N, num_trials=num_trials)
# 绘制概率图表
plot_probability(probabilities)
0x03 结果 & 结论#
得到的结果有点多,笔者仅展示有特点的几个( $N = 2,3,4,5,10,20$ )。
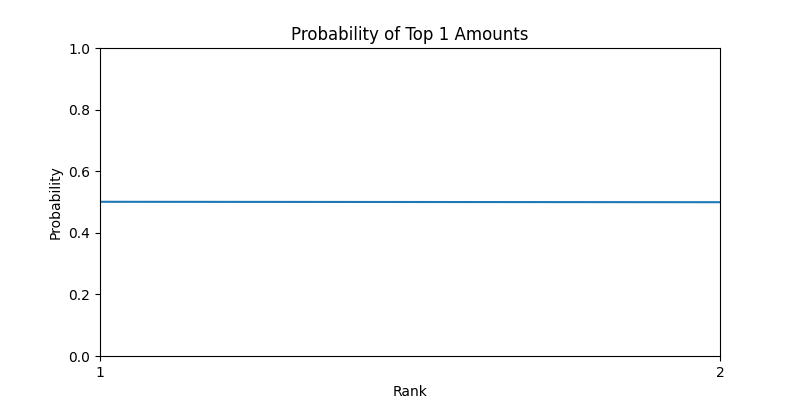
N=2
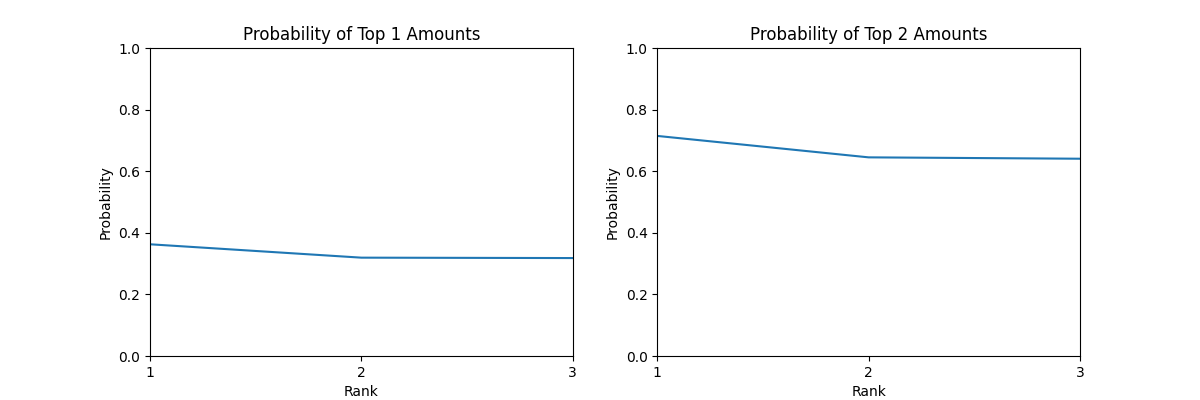
N=3
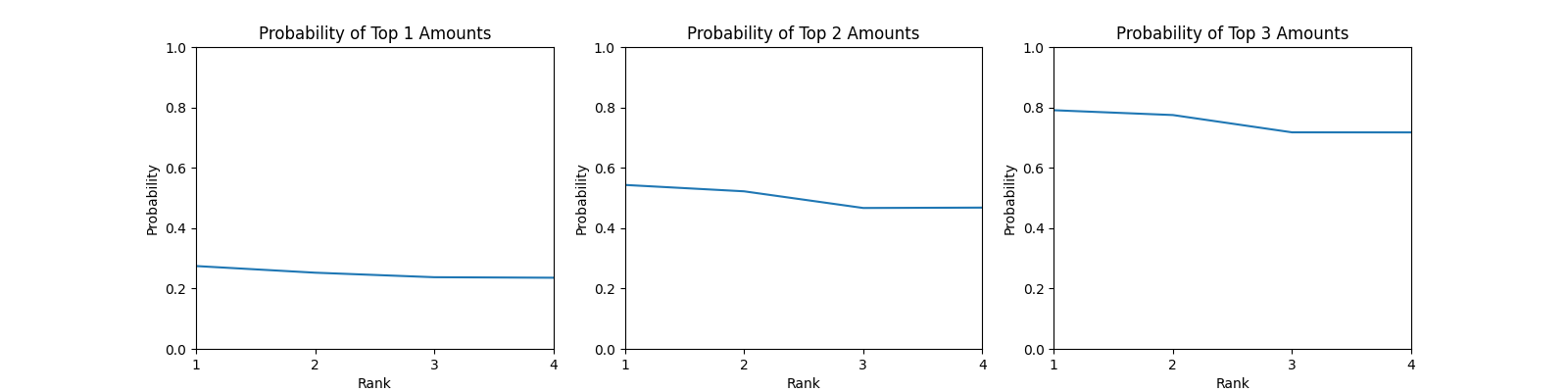
N=4
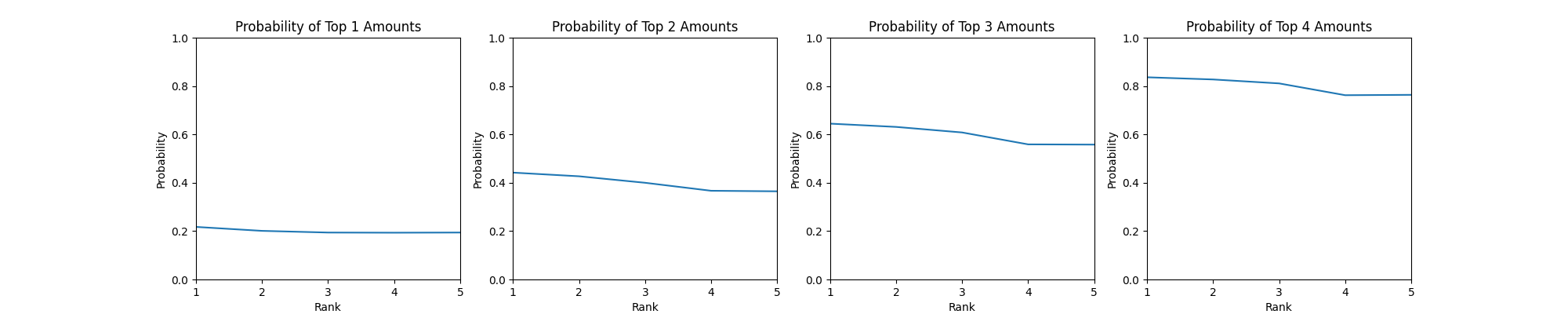
N=5
N=10
N=20
首先 Top1 其实就是运气王啦,用来和毕导得到的结果比较,验证我的结果是否是正确的。
关于运气王,也正如毕导所得到的结论,当人数越多时,后两个人获得运气王的概率越大。
关于 Top K,当 K 增加时,这个曲线会逐渐从一个下凹的曲线变成一个上凸的曲线,直到最后会变成一个单调下降的曲线。这也就是所谓的方差变大,当 K 增加时,最后一名获得较低金额的概率会变大,因而获得 Top K 的概率会变小。同时,这个 Top K 的概率也会随着 K 的增长,概率的均值变大,毕竟你 10 个人获得 Top 10 的概率始终为 1。
也就是说,在一定范围内,你获得 Top K 应当是越晚抽越好,但是当 K 超过一定值时,应当是越早抽越好。
那么这个阈值应当存在于什么地方呢?接下来来探究一下这个问题。
这里其实是有一些小 trick,首先最后一个抽红包的一定是一个非常特殊的,因为他获得的金额并不是通过采样得到的。笔者这里计算转折点时,如果考虑让整个序列单调下降,那么这个序列是极其不稳定的,甚至没有太多的规律(非递增),可能需要更多的理论计算才能支撑得到这个结论,同时也受到了很大的采样误差的影响,因为最后两个的概率差异并不大,这里笔者受概率论知识限制,将这个难题留给读者思考。但如果不考虑最后一个,只考虑前面的序列递减的话,那么这个阈值就变成了随着 N 的增加递增的了。
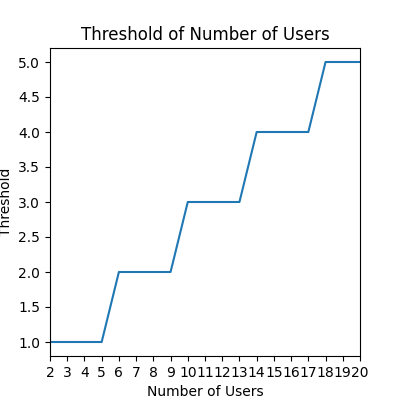
绘制的 N 关于阈值 k 的图如下所示:
曲线变化阈值 k 关于 N的曲线
一个猜测的结论就是这个阈值 k 满足下面的公式:
$$
k = \left \lfloor \frac{N-1}{4} \right \rfloor
$$
至于为什么是 4,应该是与微信红包的金额分布有关,但这里笔者缺少理论分析。
0x04 局限性#
这个其实是一个大家对立的 setting,在抽红包的过程中,大家不进行信息共享,但是是在真实环境中,你可以通过询问已抽过红包的同学获得当前的人数以及剩余金额,那么这种条件下决策则会更为复杂。比如说,前面的人抽到的都是小红包,此时决策应当是什么样子;前面有人抽到了一个很大的红包,此时决策应当是什么样子。这个问题还有待探究,留给读者思考。
这其中其实也还有很多未研究透彻的点,同时受笔者概率知识限制,难以给出更多的概率理论计算,读者若感兴趣,欢迎在评论区讨论和交流。